Surface Areas and Volumes ⇒⇒ Exercise 11.3

Question 1

Find the volume of the right circular cone with
(i) radius 6 cm, height 7 cm
(ii) radius 3.5 cm, height 12 cm

Solution :

Volume of the right circular cone = ${ 1 \over 3}{ \pi}× r^2 h$

(i) Radius 6 cm, Height 7 cm

V= $ { 1 \over 3}{ \pi} r^2 h$.

$$⇒ { 1 \over 3} × { 22 \over 7} × 6 × 6 × 7 $$

$$⇒ 22 × 2 × 6 $$

$$⇒ 22 × 12 $$

$$⇒ 264 cm^2 $$

The volume of the cone is = $ {264 } cm^3 $

(ii) radius 3.5 cm, height 12 cm

V= $ { 1 \over 3}{ \pi} r^2 h$.

$$⇒ { 1 \over 3} × { 22 \over 7} × 3.5 × 3.5 × 12 $$

$$⇒ 22 × 0.5 × 3.5 × 4 $$

$$⇒ 22 × 7 $$

$$⇒ 154 cm^2 $$

The volume of the cone is = $ {154 } cm^3 $

Question 2

Find the capacity in liters of a conical vessel with
radius 7cm, slant height 25 cm
height 12 cm, slant height 13 cm (Assume π = 22/7)

Solution :

Volume of the right circular cone = ${ 1 \over 3}{ \pi}× r^2 h$

(i) Radius 7 cm, Slant Height 25 cm

Here, we are given the radius (r) and slant height (l),
but we need the height (h) to find the volume. We can find the height using the Pythagorean theorem.

( It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.)

$$ l^2 = r^2 + h^2 $$

$$⇒ h^2 = (l)^2 - (r)^2 $$

$$⇒ h = { \sqrt {(25)^2 - (7)^2} } $$

$$⇒ h = { \sqrt { 625 - 49 }} $$

$$⇒ h = { 24} $$

Calculate the volume

V= $ { 1 \over 3}{ \pi} r^2 h$.

$$⇒ { 1 \over 3} × { 22 \over 7} × 7 × 7 × 24 $$

$$⇒ 22 × 7 × 8 $$

$$⇒ 22 × 56 $$

$$⇒ 1232 cm^3 $$

The volume of the cone is = $ {1232 } cm^3 $

Convert to liters:

$$⇒ { 1232 \over 1000} $$

( because 1L = 1000 $ cm^3 $)

$$ 1.232 L $$

The capacity of the conical vessel is 1.232 liters.

(ii) height 12 cm, slant height 13 cm

Here, we are given the height (h) and slant height (l),
but we need the radius (r) to find the volume. We can find the radius using the Pythagorean theorem.

( It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.)

$$ l^2 = r^2 + h^2 $$

$$⇒ r^2 = (l)^2 - (h)^2 $$

$$⇒ r = { \sqrt {(13)^2 - (12)^2} } $$

$$⇒ r = { \sqrt { 169 - 144 }} $$

$$⇒ r = { 5} $$

Calculate the volume

V= $ { 1 \over 3}{ \pi} r^2 h$.

$$⇒ { 1 \over 3} × { 22 \over 7} × 5 × 5 × 12 $$

$$⇒ { 22 \over 7} × 5 × 5 × 4 $$

$$⇒ { 2200 \over 7} $$

$$⇒ 314.29  cm^3 $$

The volume of the cone is = $ {314.29 } cm^3 $

Convert to liters:

$$⇒ { 314.29 \over 1000} $$

( because 1L = 1000 $ cm^3 $)

$$ 0.314 L $$

The capacity of the conical vessel is 0.314 Liters.

Question 3

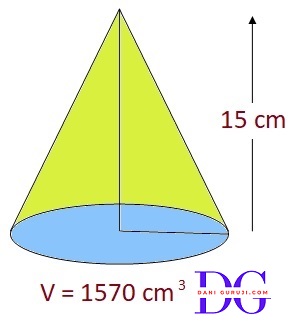
The height of a cone is 15cm. If its volume is 1570 $ cm^3 $, find the diameter of its base. (Use π = 3.14)

Solution :

Volume of the right circular cone = ${ 1 \over 3}{ \pi}× r^2 h$

To find the diameter, we first need to find the radius (r). We can rearrange the formula to solve for r

$$ r^2= { {3V} \over { \pi h }}$$

$$⇒ r^2= { {3 × 1570} \over { 3.14 × 15 }}$$

$$⇒ r^2= { {4710} \over { 47.10 }}$$

$$⇒ r^2= 100 $$

$$⇒ r = 10 $$

The radius of the right circular cone is = $ {10 } cm $

3. Finding the Diameter

The diameter (d) is twice the radius

d = 2 × 10 cm

Diameter = 20 cm.

Question 4

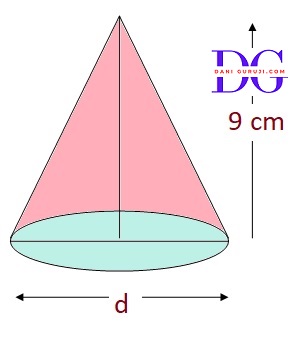
If the volume of a right circular cone of height 9cm is 48π$ cm^3 $, find the diameter of its base. (Use π = 3.14)

Solution :

Volume of the right circular cone = ${ 1 \over 3}{ \pi}× r^2 h$

To find the diameter, we first need to find the radius (r).

$$ V = $ { 1 \over 3}{ \pi} r^2 h$$

$$⇒ 48{ \pi} = { 1 \over 3} × { \pi} × r^2 × 9 $$

$$⇒ r^2= { {48 × 3 } \over {9 }}$$

$$⇒ r^2= { 16}$$

$$⇒ r = 4 $$

The radius of the right circular cone is = $ {4 } cm $

3. Finding the Diameter

The diameter (d) is twice the radius

d = 2 × 4 cm

Diameter = 8 cm.

Question 5

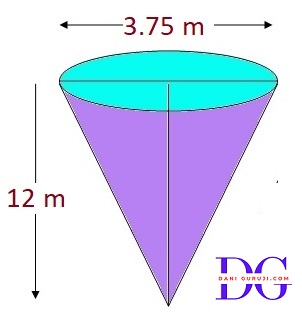
A conical pit of top diameter 3.5m is 12m deep. What is its capacity in kiloliters? (Assume π = 22/7)

Solution :

The diameter of the conical pit is given as 3.5 m. The radius (r) is half of the diameter

$$⇒ r = { 3.5 \over 2} $$

$$⇒ r = 1.75 m $$

Height of pit, h = Depth of pit = 12m

Calculate the Volume

$$ V = { 1 \over 3}{ \pi} r^2 h $$

$$⇒ { 1 \over 3} × { 22 \over 7} × (1.75)^2 × 12 $$

$$⇒ { 1 \over 3} × { 22 \over 7} × 1.75 × 1.75 × 12 $$

$$⇒ 22 × 0.25 × 1.75 × 4 $$

$$⇒ V = 38.5 m^3 $$

Convert to kiloliters:

$$⇒ {38.5} × 1 $$

( because 1$m^3 $= 1000L = 1kl )

$$ 38.5 kiloliters $$

Hence, capacity of the pit is 38.5 kiloliters

Question 6

The volume of a right circular cone is 9856 $ cm^3 $. If the diameter of the base is 28cm,
find height of the cone
slant height of the cone
curved surface area of the cone . (Assume π = 22/7)

Solution :

The diameter of the cone is given as 28 cm. The radius (r) is half of the diameter

$$⇒ r = { 28 \over 2} $$

$$⇒ r = 14 cm $$

Volume of a right circular cone = 9856 $ cm^3 $

Calculate the Height (h)

$$ V = { 1 \over 3}{ \pi} r^2 h $$

$$ 9856 = { { 1 \over 3} × { 22 \over 7} × (14)^2 × h } $$

$$ h = {{9856 × 3} \over {{ 22 \over 7} × (14)^2 }} $$

$$ h = {{9856 × 3 } \over {{ 22 \over 7} × 196 }} $$

$$ h = {{29,568} \over { 22 × 28 } } $$

$$ h = {{29,568} \over { 616 } } $$

$$ h = 48 $$

The height of the cone is 48 cm.

(ii)Calculate the Slant Height (l)

The slant height, radius, and height of a right circular cone form a right-angled triangle. We can use the Pythagorean theorem to find the slant height:

$$ ⇒ { l^2 = h^2 + r^2 } $$

$$ ⇒ { l^2 = (48)^2 + (14)^2 } $$

$$ ⇒ { l^2 = (2304 + 196 )} $$

$$ ⇒ l = {\sqrt{2500 } } $$

$$⇒ l = 50 cm $$

Therefore, The slant height of the cone is 50 cm.

(iii) Calculate the Curved Surface Area

Curved surface area of the cone = πrl

$$ CSA = { { 22 \over 7} × 14 × 50 } $$

$$⇒ { 22 × 2 × 50 } $$

$$⇒ { 2200 }cm ^2 $$

Curved surface area of the cone: ${ 2200 }cm ^2 $

Question 7

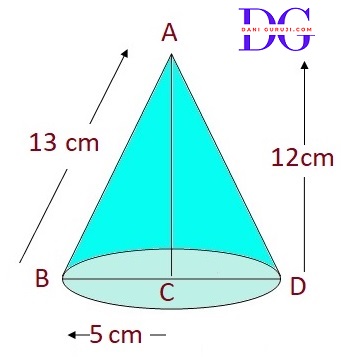
A right triangle ABC with sides 5cm, 12cm and 13cm is revolved about the side 12 cm. Find the volume of the solid so obtained.

Solution :

The triangle with sides 5cm, 12cm, and 13cm is revolved around the 12cm side.

The side it's revolved about becomes the height (h) of the cone. So, h = 12 cm.

The other perpendicular side becomes the radius (r) of the cone's base. So, r = 5 cm

The hypotenuse (13cm) is the slant height,

Calculate the Volume

$$ V = { 1 \over 3}{ \pi} r^2 h $$

$$⇒ { 1 \over 3} × { \pi} × (5)^2 × 12 $$

$$⇒ { 1 \over 3} × { \pi} × 5 × 5 × 12 $$

$$⇒ {{ \pi} × 25 × 4} $$

$$⇒ { 100{ \pi}} $$

$$⇒ V = { 100{ \pi}} cm^3 $$

The volume of the solid obtained is approximately $ { 100{ \pi}} cm^3 $

Question 8

If the triangle ABC in the Question 7 is revolved about the side 5cm, then find the volume of the solids so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.

Solution :

A right-angled ΔABC is revolved about its side 5cm, a cone will be formed of radius as 12 cm, height as 5 cm, and slant height as 13 cm.

Calculate the Volume

$$ V = { 1 \over 3}{ \pi} r^2 h $$

$$⇒ { 1 \over 3} × { \pi} × (12)^2 × 5 $$

$$⇒ { 1 \over 3} × { \pi} × 12 × 12 × 5 $$

$$⇒ {{ \pi} × 60 × 4} $$

$$⇒ { 240{ \pi}} $$

$$⇒ V = { 240{ \pi}} cm^3 $$

The volume of the solid obtained is approximately ${ 240{ \pi}} cm^3 $

So, required ratio =

(result of question 7) / (result of question 8)

$$ ⇒ { { 100{ \pi}} \over { 240{ \pi}}} $$

$$⇒ { 5 \over 12} $$

Question 9

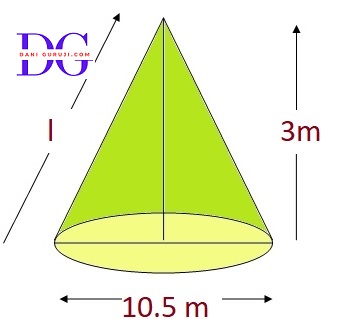
A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas.

Solution :

The diameter of the cone is given as 10.5 m. The radius (r) is half of the diameter

$$⇒ r = { 10.5  \over 2} $$

$$⇒ r = 5.25 m $$

Height (h) = 3 m

Calculate the Volume of heap

$$ V = { 1 \over 3}{ \pi} r^2 h $$

$$⇒ { 1 \over 3} × { \pi} × (5.25)^2 × 3 $$

$$⇒ { 1 \over 3} × { 22 \over 7} × 5.25 × 5.25 × 3 $$

$$⇒ { 1 \over 3} × {22 × 0.75 × 5.25 × 3} $$

$$⇒ {22 × 0.75 × 5.25 } $$

$$⇒ V = { 86.625} m^3 $$

Volume of heap = ${ 86.625} m^3 $

Calculate the Area of the Canvas

The canvas will cover the curved surface of the heap. To find this area (A),

Curved surface area of the cone = πrl

where l is the slant height.

First, we need to find the slant height (l) using the Pythagorean theorem with the radius and height:

$$ ⇒ { l^2 = h^2 + r^2 } $$

$$ ⇒ { l^2 = (5.25)^2 + (3)^2 } $$

$$ ⇒ { l^2 = (27.562 + 9 )} $$

$$ ⇒ l = {\sqrt{36.562 } } $$

$$⇒ l = 6.046m $$

Therefore, The slant height of the cone is approximately 6.05m.

Now we can calculate the area of the canvas:

$$ CSA = { { 22 \over 7} × 5.25 ×6.05 } $$

$$⇒ { 22 × 0.75 × 6.05 } $$

$$⇒ { 99.82 }m ^2 $$

Thus, the required area of the canvas is : ${ 99.82 }m ^2 $